1. Calculate the following:
    1. -5 – (3) (-2)
    2. 7/12 + 2/3 – 1/4
    3. 14 5/6 – (-7 2/3)
    4. 3(-2) – 5(-3) – (-2)$^2$
    5. 3.5 – 0.05(2) +14.2 / 0.2
    6. $(\sqrt{169} – \sqrt{64}) / 2 \sqrt{25}$
    7. |5| x |-2| – |-8|
  2. Evaluate each of the following if x = -3 and y = 2:
    1. $3x^2 – 2y^3$
    2. $x^3 – xy – 3$
  3. Find:
    1. N if 40% of N is 16
  4. Solve:
    1. 7x – 3 – 2x = 2(x+3)
  5. Simplify the following:
    1. $(4x – 2y)^2$
    2. $(3/2x + 3)(1/2x – 3)$
  6. Solve:
    1. 2x – 4 < 5x + 8
  7. Factor the following completely:
    1. $12a^5 – 18a^4 – 6a^3$
    2. $3(2x – 1) – 4y (2x – 1)$
  8. Solve the system below:
    $\begin{cases} 3x – 2y = 7\\ 5x + 2y = 1\\ \end{cases}$
  9. Simplify and state restrictions:
    $\frac{5x^2 – 10x}{x^2 – 5x + 6} \div \frac{2x^2 + 6x}{x^2 – 9}$
  10. Solve for $x{,} x \ne 0{,} x \ne -3$:$\frac{3x – 4}{x} – \frac{x+1}{x+3} = 2$
  11. Find:
    1. the length and the slope of the line segment connecting A(3, 5) and B(-3, 4)
  12. Graph:
    1. 2x + 5y = 10
  13. Graph:
    1. $y = 2x^2$
  14. Find x, y, z, w:
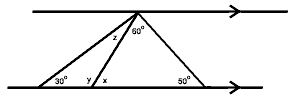
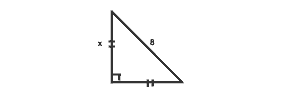
  15. Solve the following equations for x or y:
    1. $2^{x+1}=8 $
    2. $2x^2 – 3x –
      5 = 0 $
    3. $x/4 = 3/y = 5/30 $
  16. Find:
    1. The tenth term of an arithmetic sequence when its first term is 3 and the common difference is 2.
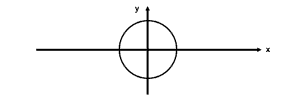
  17. Find the area of the following figures:
    1. $x^2 + y^2 = 16$
    2. AD = 3cm, BC = 5cm, AE = 2cm
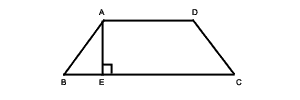
  18. Graph each of the following:
    1. $y = -x^2 + 2 $
    2. $y = 2^x$
    3. $y = sin(1/2x) + 2, 0\le x \le 2\pi $
  19. Simplify:
    1. $\frac{2^{-3} \ x \ 4^{2}}{16^{-1}}$
    2. $5\sqrt{a^{3 \ 4}\sqrt{a}}$
    3. log 75 – log 3 + log 4
    4. $\frac{sin x \ + \ tan x}{sin^2x + cos^2+cos z}$
  20. Solve:
    1. |x – 3| = 5
    2. $2^{2x} – 12(2^x) + 32 = 0 $
  21. Divide:
    1. $x^3 + 7x^2 – 11x + 4 by x + 5 $